Yet another smoothing (curve-fitting) algorithm?

We needed a super-efficient, real-time line smoothing algorithm for jSignature. It captures the signature as vectors by storing pointer (mouse, finger, stylus) coordinates into "stroke" arrays. These can be rendered on document at high resolution using post-production line smoothing (de-noising (simplification) + curve fitting), but while the signature is captured, we need to show something pleasant on the screen that approximates the stroke movement and later-to-be-rendered image.

Traditional "wait till you have the entire sequence, then analyze" algorithms don't fit this real-time smoothing model. We needed a logic that would introduce no perceived lag between movement and stroke rendering. A lot of other "real-time" algorithms ride on top of "inertia" or "iterative least error" calculations. Most of these introduce an observable lag in rendering, and some introduces a minor, but noticeable re-rendering path corrections in tail of the stroke. Combined with CPU cycles spent on simulated variable stroke thickness the solutions offered out there were too inefficient for our intended use of jSignature in mobile browsers.

A compounding problem with many published line smoothing algorithms is that they often require a advanced degree of skill and understanding to implement and maintain the smoothing algorithm. Since jSignature is an open-source component, understanding of the smoothing code by "average" code contributor was important for stability and maintainability of the project.

Getting to efficient stroke smoothing algorithm

What we came up with is a computationally-efficient method of fitting Bezier curves between two points composed of (a) holding vectors parallel to lines crossing the points surrounding the curves' junction point, and (b) deriving the lengths of control point handles based on the angle formed at the junction point.

Holding the vectors of control points emanating from two curves' junction point as lying on the same line is not new, as that is the only way to force one Bezier curve flow into another without visible kink at the junction point.

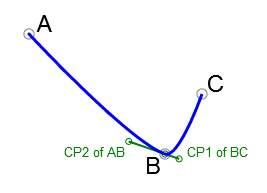
Equally not new, but less intuitive is the idea of holding these control points' vectors parallel to the line connecting the points immediately surrounding the targeted point.

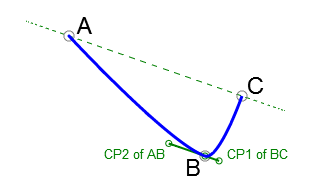
What we see a lot of variation in is the method of determining the length of the control points' vectors, leading to degree of rounding occurring at that point. Many algorithms somehow infer the length of control points' vectors from the distances among the target point and the points immediately preceding and following it. But, in almost all of those cases the lengths of the control points' vectors are not affected by the angle formed at the target point. This often leads to unnatural bubbling around what otherwise should be sharp points in drawing strokes.

Our efficient curve-fitting algorithm

What we have assembled is an efficient method of inferring the lengths of control points' vectors based on the angle formed at the two curves' junction point formed by two lines connecting Preceding, Junction and Following endpoints of the two curves. Together with alignment of the control point vectors with the line crossing the points directly surrounding the junction point, this forms a tremendously simple way of describing the sections of two curves forming a junction point.

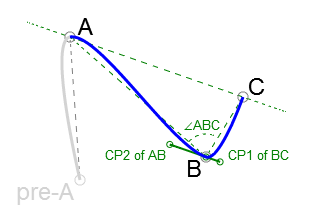
We found that to achieve a natural, visually pleasing junction between two Bezier curves (let's call them AB and BC), going from point A, connected at junction point B, and ending at point C, the lengths of the control points' vectors emanating from junction point B (let's call these control point vectors BtoCP2ofAB and BtoCP1ofBC) must be equal to

ABCAngleDerivativeRatio x VectorLength

where VectorLength is separately the length of vector AB and BC (for vectors BtoCP2ofAB and BtoCP1ofBC respectively), and where ABCAngleDerivativeRatio is derived as

| ABCAngle | x ( LimitTop - LimitBottom )  + LimitBottom 

where ABCAngle is the angle between BA and BC vectors measured in PI and is in the range from -1 to +1, and where LimitTop and LimitBottom are ratios in a certain range.

There, LimitBottom establishes the minimum length of a control point handle as a percentage of length of a curve that control point handle describes, and LimitTop establishes the maximum length of such a control point handle.

We deem such range from about 35% (0.35) to about 10% (0.10) to be most pleasing to the eye when pointing device capture units approximately equal rendering units (i.e. mouse movement detection VS. screen pixels). We recommend to lower the LimitBottom ratio to about 2% (0.02) when, before rendering, captured strokes are to be scaled up to resolution higher than that of a capture device.

This algorithm for deriving the length of the control points emanating from the curves' junction point allows to achieve "natural," "pleasing" smoothing at the curves' junction that varies dynamically throughout other junction points on a path formed of multiple curves, while still allowing for permanent real-time rendering of all but last 2 curves in the path. Smoothing of the strokes in this manner does not introduce noticeable lag between the movement of the pointing device and the rendering of the stroke following it.

De-noising (simplifying) the stroke before smoothing

One worthy addition to this algorithm is real-time de-noising of the curve endpoint data. Before the above algorithm is invoked, a filter may be introduced between the "pointer moved to point X" event generator and the above-mentioned curve fitting algorithm. In our current case, we do not convey the "pointer moved to point X" events to the rendering logic until the distance from prior curve's end-point exceeds 2 units (i.e. "browser pixels") of movement.

Diagonal movement over a square-unit grid may generate superfluous capture-device-induced noise (often referred to as 'aliasing artifacts'). Our ignoring of sub-2-capture-units movements allows the above-mentioned curve-fitting algorithm to do a better job of inferring the true intent of the pointing device's movement across the capture grid and to do a better job of representing that movement intents as rendered, smoothed, anti-aliased strokes.

Efficient variable pen pressure simulation

Another additional improvement to the presentation of the rendered strokes is the use of asymmetric brush for painting of the strokes as an efficient, simple way to simulate variable pen pressure.

The best such asymmetric brush is an oval slanted diagonally and locked in that slant regardless of direction of the stroke. As a result, depending on the direction of the stroke, the width of the stroke automatically thickens or slims consistently with the direction of the stroke, simulating heavier or lighter pen pressure on down or sideways strokes.

One very efficient way such asymmetric brush can be simulated on rendering interfaces where rendering of Bezier curves cannot be done with asymmetric brush of fixed orientation, is to shadow the original curve with another that is offset diagonally by some half of the stroke's width. Another, somewhat more demanding for the rendering device, way of simulating such asymmetric brush is to close the original and diagonally-offset curves into a shape and fill it with color.

Artificial pressure stroke thickening algorithms based on inertia, or movement speed, or point sparsity were found by us as less efficient and, most-importantly, inconsistent, and thus, appearing unnatural, on similarly slanted strokes.